Description
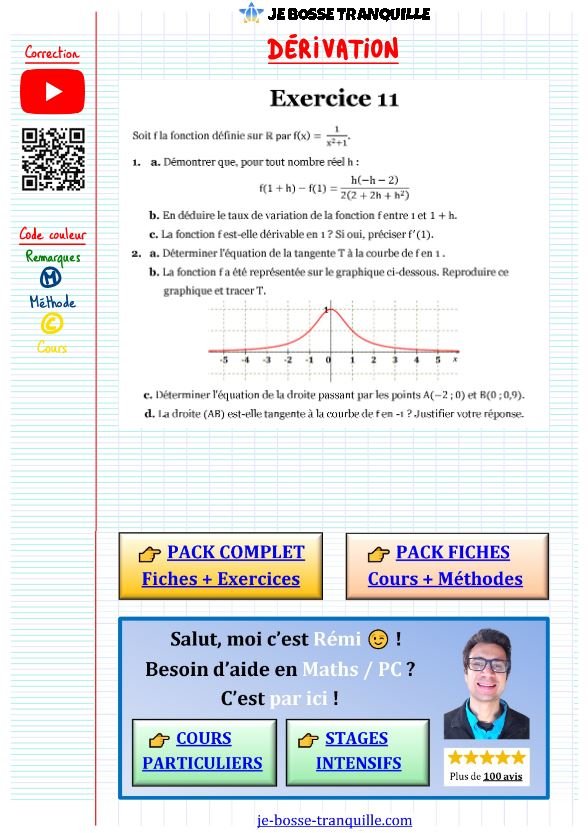
Cet exercice nombre derivé et tangente te confronte aux défis passionnants de la dérivation d’une fonction rationnelle f(x) = 1/(x²+1).
Tu vas découvrir comment manipuler le taux d’accroissement d’une fonction pour démontrer une égalité importante et en déduire la dérivabilité en un point.
Compétences que tu développeras :
- Calcul du taux de variation d’une fonction rationnelle
- Détermination de limites et dérivabilité en un point
- Équation de tangente à une courbe
- Analyse graphique et positions relatives
La correction est structurée en étapes progressives 🧩, partant du calcul de f(1+h)-f(1) jusqu’à la détermination de l’équation y = -0,5x + 1 de la tangente au point d’abscisse 1.
Tu apprécieras la clarté des calculs pour transformer les expressions complexes en formules élégantes, comme la simplification du taux de variation pour obtenir τ(h) = -h-2/2(h²+2h+2).
La correction vidéo de cet exercice nombre derivé et tangente te guide comme un prof particulier, t’expliquant chaque manipulation algébrique avec précision.
Ces notions sont fondamentales en analyse et te serviront tout au long de ton parcours en mathématiques !
Disponible en PDF détaillé ou en vidéo explicative pour maîtriser parfaitement ces techniques essentielles. ✏️