Description
Cet exercice math integrale corrige te fait explorer la fascinante famille de fonctions fₙ(x) = x^n e^-x et leurs intégrales sur [0,1]. 📈
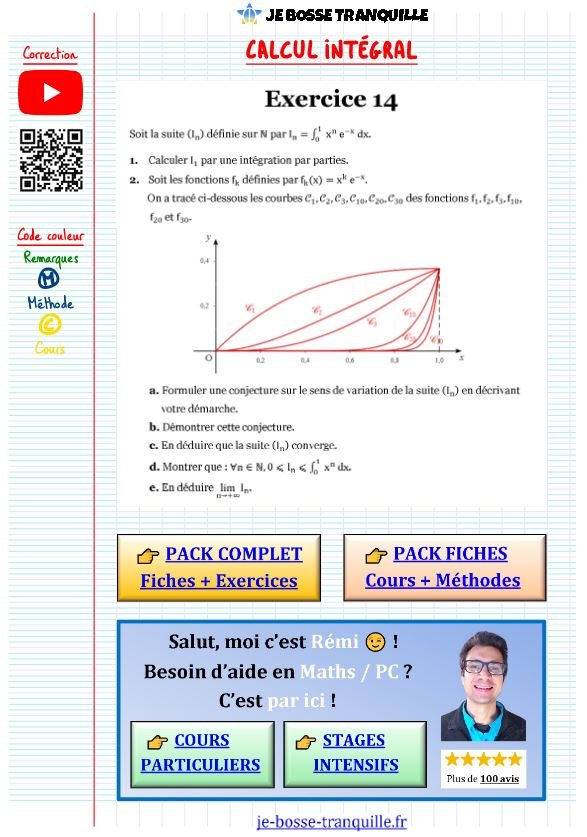
Tu travailleras sur la suite (Iₙ) définie par Iₙ = ∫₀¹ x^n e^-x dx, qui combine exponentielle et puissances pour développer une intuition mathématique solide.
Compétences que tu développeras :
- Maîtrise de l’intégration par parties avec paramètre
- Analyse du sens de variation d’une suite définie par des intégrales
- Utilisation de l’interprétation graphique pour formuler des conjectures
La correction est structurée de façon progressive, commençant par le calcul de I₁ par intégration par parties pour obtenir I₁ = 1 – 2e^-1.
Tu découvriras comment passer de l’observation graphique à la démonstration rigoureuse que la suite (Iₙ) est décroissante.
En vidéo, cet exercice math integrale corrige c’est comme avoir un prof qui t’explique les liens entre courbes et intégrales et te montre pourquoi les aires sous les courbes diminuent. 🔍
Tu comprendras l’astuce pour prouver que 0 < Iₙ < ∫₀^∞ x^n e^-x dx et en déduire la limite de la suite.
Ces techniques sont essentielles pour les épreuves de spécialité où l’on attend de toi que tu saches combiner calcul, analyse et interprétation graphique.