Description
Ce pack « Fiche de revision maths terminale » (Complet) contient toutes les fiches nécessaires pour maîtriser le programme de maths de terminale :
– 9 Fiche de Cours
- Vecteurs, droites et plans de l’espace
- Orthogonalité et distances dans l’espace
- Suites
- Continuité
- Dérivation et convexité
- Limites de fonctions
- Logarithme népérien
- Primitives et équations différentielles
- Loi binomiale
– 68 Fiches Méthodes
– Suites (terminale)
- Déterminer la limite d’une suite : Somme
- Déterminer la limite d’une suite : Produit
- Déterminer la limite d’une suite : Quotient
- Déterminer la limite d’une suite : Encadrement
- Déterminer la limite d’une suite : Composition
- Déterminer la limite d’une suite géométrique
- Utiliser le raisonnement par récurrence
- Montrer qu’une suite est convergente
- Montrer qu’une suite auxiliaire est géométrique
- Déterminer le plus petit entier tel que un > a (algorithme)
- Déterminer le plus petit entier tel que un > a (calculatrice)
- Etudier le sens de variation d’une suite (1ère)
– Géométrie
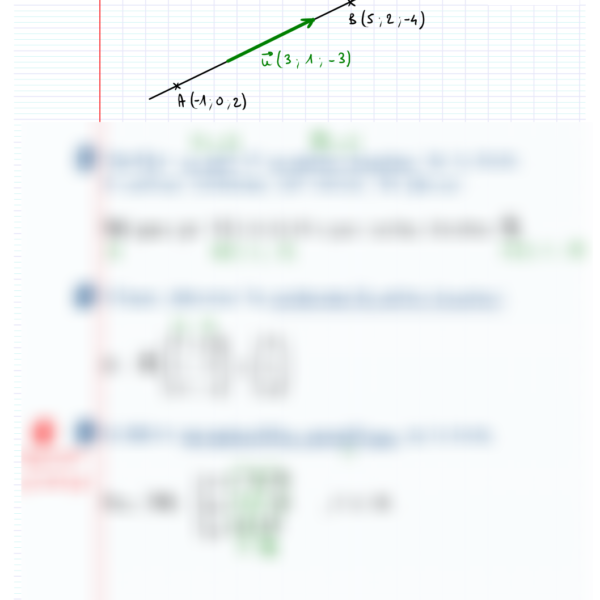
- Déterminer la représentation paramétrique d’une droite
- Déterminer les coordonnées de points dans l’espace
- Déterminer si deux droites sont parallèles dans l’espace
- Déterminer si deux droites sont sécantes dans l’espace
- Déterminer si deux vecteurs sont colinéaires
- Déterminer si trois vecteurs sont coplanaires
- Déterminer si un point appartient à une droite dans l’espace
- Exprimer un vecteur dans une base de l’espace
- Calculer l’aire d’un triangle (espace)
- Calculer le volume d’un tétraèdre
- Calculer un angle à l’aide du produit scalaire
- Déterminer le point d’intersection entre une droite et un plan
- Déterminer les coordonnées du projeté orthogonal d’un point sur une droite – Polynôme
- Déterminer les coordonnées du projeté orthogonal d’un point sur une droite – Système
- Déterminer si deux vecteurs sont orthogonaux
- Déterminer une équation cartésienne d’un plan
- Montrer qu’un vecteur est normal à un plan
– Fonctions
- Etudier la continuité d’une fonction en un point
- Montrer que f(x) = k admet une unique solution
- Déterminer le nombre de solutions de f(x) = k
- Donner un encadrement ou une valeur approchée de α
- Exprimer f(α) en fonction de α
- Montrer qu’un intervalle est stable
- Utiliser le théorème du point fixe pour déterminer une limite
- Dériver une fonction (1ère)
- Etudier les variations d’une fonction (1ère)
- Etudier le signe d’une expression (2de)
- Etudier la convexité d’une fonction
- Déterminer le domaine de définition d’une fonction (1ère)
- Déterminer l’équation réduite de la tangente à une courbe (1ère)
- Etudier la position relative de deux courbes (1ère)
- Déterminer la limite d’une fonction : Somme
- Déterminer la limite d’une fonction : Produit
- Déterminer la limite d’une fonction : Quotient
- Déterminer la limite d’une fonction : Composition
- Déterminer la limite d’une fonction : Encadrement
- Montrer qu’une droite est asymptote à une courbe
- Résoudre une (in)équation avec la fonction ln
- Déterminer le plus petit entier tel que un > a (logarithme)
– Primitives et équations différentielles
- Résoudre une équation différentielle de la forme y’=ay+b
- Déterminer une solution particulière d’une équation différentielle
- Montrer qu’une fonction est solution d’une équation différentielle
- Montrer que deux équations différentielles sont équivalentes
- Montrer qu’une fonction est une primitive
– Probabilités
- Montrer qu’une variable aléatoire suit une loi binomiale
- Calculer l’espérance d’une variable aléatoire (loi binomiale)
- Calculer P(X=a) avec une calculatrice
- Calculer P(X≤a) avec une calculatrice
- Calculer P(X≥a)
- Calculer P(a≤X≤b)
- Résoudre P(X≤a)≥b avec une calculatrice
- Déterminer la loi de probabilité d’une variable aléatoire (1ère)
- Construire un arbre pondéré (1ère)
- Calculer une probabilité à l’aide d’un arbre pondéré (1ère)
- Calculer une probabilité conditionnelle (1ère)
- Utiliser la loi des probabilités totales avec un arbre pondéré (1ère)
Ce pack « Fiche de revision maths terminale » contient les packs suivants :