Description
Cet exercice suite numérique te fait découvrir l’art de l’analyse graphique d’une suite représentée par une fonction ! 📊
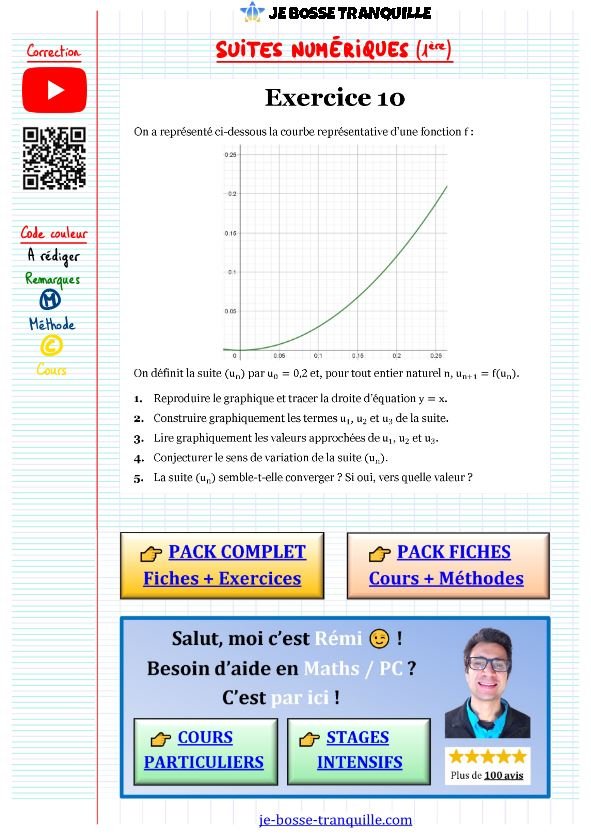
Tu exploreras comment une courbe peut révéler tous les secrets d’une suite définie par uₙ = 0,2 et uₙ₊₁ = f(uₙ).
Compétences que tu développeras :
- Lecture graphique de termes successifs d’une suite
- Construction graphique des termes u₁, u₂, u₃ et u₄
- Conjecture du sens de variation à partir du graphique
- Analyse de la convergence d’une suite récurrente
- Interprétation graphique de la limite d’une suite
La correction détaillée te guide dans la technique du « graphique en escalier » : tu partiras de u₀ = 0,2 sur l’axe des x pour construire visuellement chaque terme. 🔄
Tu découvriras dans cet exercice suite numérique comment les valeurs oscillent autour de la limite : u₁ = 0,10, u₂ = 0,042, u₃ = 0,005…
Le graphique révélera que la suite est strictement décroissante et converge vers 0 !
La vidéo explicative décompose chaque construction graphique avec précision, comme un cours particulier interactif.
Disponible en PDF illustré ou en vidéo animée pour maîtriser totalement cette technique visuelle.