Description
Cet exercice premiere produit scalaire te propose de démontrer la perpendicularité de deux droites dans un triangle rectangle et isocèle, en utilisant deux approches différentes.
Tu découvriras comment exploiter le produit scalaire pour prouver qu’un même résultat géométrique peut être obtenu par différentes méthodes mathématiques.
Compétences que tu développeras :
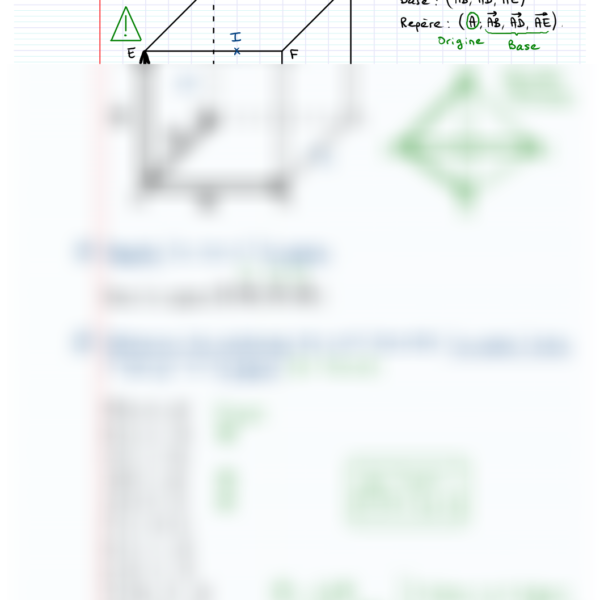
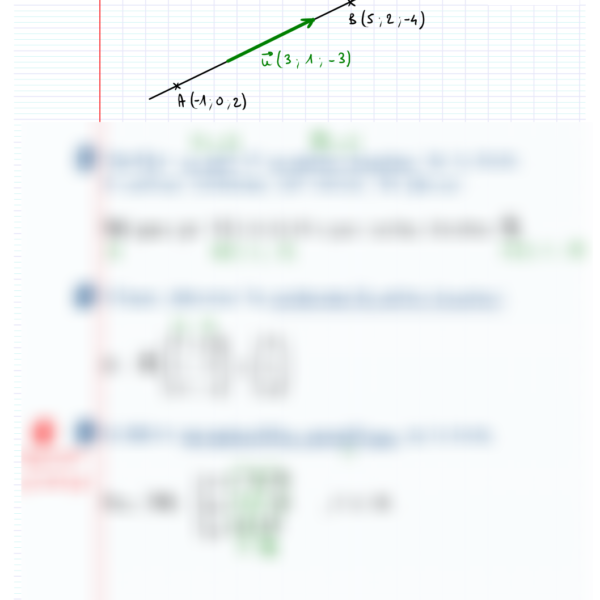
- Utilisation de coordonnées dans un repère orthonormé
- Exploitation de propriétés du triangle rectangle et isocèle
- Calcul de produit scalaire pour démontrer une orthogonalité
- Application de relations vectorielles comme I est le milieu de [CM]
La correction est structurée en deux méthodes complémentaires, te montrant la richesse des approches possibles en géométrie.
Tu verras d’abord comment utiliser les coordonnées dans un repère pour calculer AI⃗·BN⃗ = 0, puis comment exploiter la décomposition vectorielle AI⃗ = 1/2(AM⃗ + AC⃗) sans utiliser de repère. 🧮
La vidéo de correction de cet exercice premiere produit scalaire t’offre une explication visuelle détaillée des deux méthodes, comme si un prof te montrait pas à pas les subtilités de chaque raisonnement.
Ces techniques sont fondamentales en géométrie analytique, où la capacité à choisir la méthode la plus adaptée est une compétence précieuse !