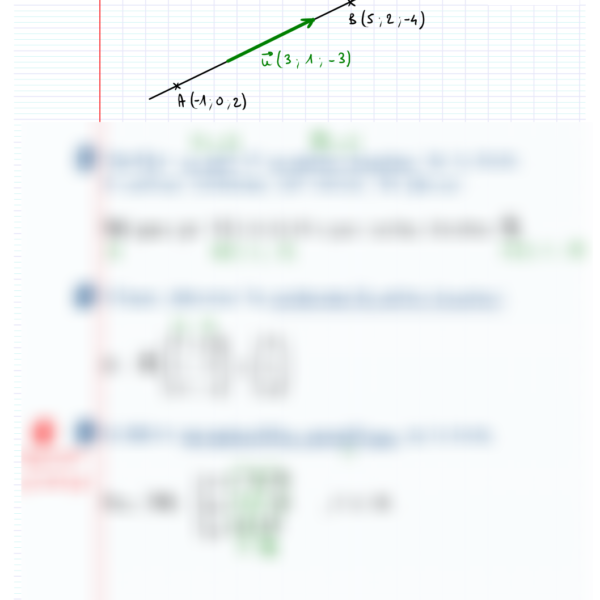
Description
Cet exercice d’application de la derivation te plonge dans une application pratique et concrète de la dérivation à travers un problème industriel de fabrication d’une boîte.
Tu exploreras comment modéliser mathématiquement le volume d’une boîte fabriquée à partir d’une plaque métallique de dimensions fixes.
Compétences que tu développeras :
- Modélisation géométrique d’un problème concret
- Construction d’une fonction volume à partir de contraintes physiques
- Dérivation et recherche d’extremums pour optimiser un volume
- Résolution d’équations du second degré avec interprétation des solutions
La correction est remarquablement claire 🔍, avec un schéma explicatif de la boîte et le développement détaillé de la fonction V(x) = 4x³ – 84x² + 432x.
Tu découvriras la transformation astucieuse de la dérivée V'(x) = 12(x² – 14x + 36) pour résoudre l’équation du second degré et trouver les valeurs x₁ ≈ 3,5 et x₂ ≈ 10,6.
La vidéo de cet exercice d’application de la derivation te guidera étape par étape, comme si un prof était à tes côtés, pour t’aider à visualiser la situation et comprendre chaque manipulation algébrique.
Ces techniques d’optimisation sont essentielles dans de nombreux domaines techniques et scientifiques !
Disponible en PDF détaillé ou en vidéo explicative pour maîtriser complètement cette méthode fondamentale. ✏️