Description
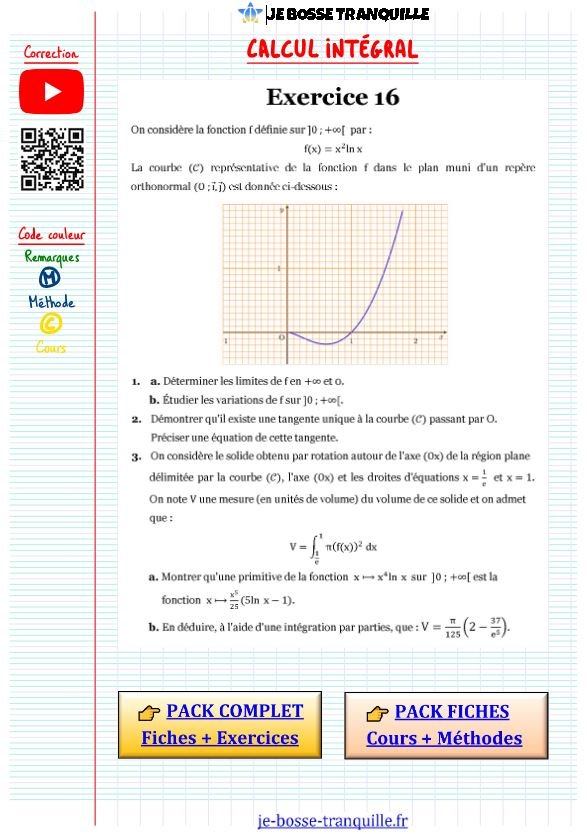
Cet exercice bac integrale te fait explorer la fonction f(x) = x² ln(x) sous tous ses angles avant de l’utiliser dans un problème concret de calcul de volume. 🌀
Tu travailleras sur cette fonction qui combine puissance et logarithme pour développer à la fois des compétences en analyse et en géométrie dans l’espace.
Compétences que tu développeras :
- Étude complète d’une fonction avec logarithme (limites, variations)
- Détermination de tangentes particulières à une courbe
- Calcul de volume d’un solide de révolution par intégration
La correction est parfaitement structurée, commençant par l’étude des limites aux bornes de l’intervalle puis l’analyse des variations avec le tableau complet.
Tu verras comment déterminer l’existence d’une tangente passant par l’origine et sa position exacte au point d’abscisse e^(-1/2).
En vidéo, cet exercice bac integrale c’est comme avoir un prof qui t’explique les astuces pour calculer une primitive de x² ln(x) et t’aide à visualiser le solide de révolution. 📊
Tu comprendras enfin comment l’intégration par parties permet d’obtenir la formule explicite du volume V = π/125 (2 – 17/e²).